Langsung ke konten utama

Pembahasan kalkulus dan geometri analitis edisi kelima jilid 1 bab 1 sub bab 1

Anda pasti masih ingat bagaimana memanipulasi bilangan, tetapi tidak ada salahnya untuk mengulang kembali sejenak. Dalam soal-soal 1-20, sederhanakan sebanyak mungkin. Pastikan untuk menghilangkan semua tanda kurung dan memudahkan semua pecahan. (kelihatannya dimulai dulu dari soal-soal yang sederhana 
  1. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 1

    1. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 39 Buktikan bahwa rata-rata dua buah bilangan terletak di antara kedua bilangan itu, artinya, buktikan bahwa:
    2. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 40 gak pusing kan.........??
    3. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 2
    4. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 3
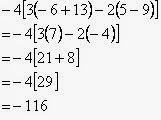
    5. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 4
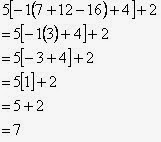
    6. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 5
    7. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 6
    8. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 7
    9. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 8
    10. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 9
    11. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 10
    12. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 11
    13. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 12
    14. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 13
    15. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 14
    16. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 15
    17. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 16
    18. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 17
    19. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 18
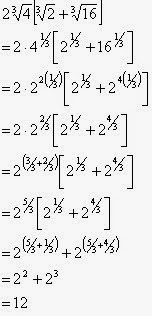
    20. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 19
    21. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 20 (gak susah kan........... ni akan dimulai soal yang pakai variabel) Sedikit latihan aljabar akan baik untuk mahasiswa kalkulus. Dalam Soal-soal 21-34, lakukan operasi yang diminta dan sederhanakan.
    22. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 21
    23. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 22
    24. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 23
    25. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 24
    26. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 25
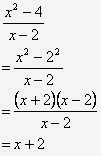
    27. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 26
    28. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 27
    29. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 28
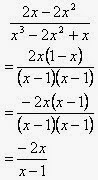
    30. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 29
    31. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 30
    32. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 31 Pembahasan no. 31 ini semula ada kekeliruan dan alhamdulillah telah dikoreksi oleh Haves Taratula, terima kasih...^_^
    33. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 32
    34. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 33
    35. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 34
    36. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 35 Carilah nilai masing-masing yang berikut; jika tak terdefinisi, katakan demikian
    37. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 36 Perlihatkan bahwa pembagian oleh 0 adalah tanpa arti sebagai berikut:
    38. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 37 Nyatakanlah apakah masing-masing yang berikut benar atau salah,
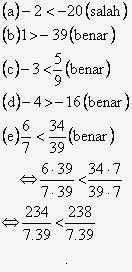
    39. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 38
 
  1. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 41
    Bilangan prima adalah bilangan asli (bilangan bulat positif) yang hanya mempunyai dua bilangan asli pembagi, bilangan itu sendiri dan 1. Beberapa bilangan prima yang pertama adalah 2, 3, 5, 7, 11, 13, 17. Menurut Teorema Dasar Hitungan, setiap bilangan asli (selain 1) dapat kita tulis sebagai hasil kali suatu himpunan unik bilangan prima. Misalnya, 45 = 3 . 3 . 5. Tuliskan masing-masing yang berikut sebagai suatu hasil kali bilangan-bilangan prima. Catatan: Hasil kali tersebut adalah trivial jika bilangan itu adalah prima – yaitu, ia hanya mempunyai satu faktor
    ( a ) 240 = 2 . 2 . 2 . 2 . 3 . 5 ( b ) 310 = 2 . 5 . 31 ( c ) 119 = 7 . 17 ( d ) 5400 = 2 . 2 . 2 . 3 . 3 . 3 . 5 . 5
  2. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 42 Gunakan Teorema Dasar Hitungan (Soal 41) untuk membuktikan bahwa kuadrat sebarang bilangan asli (selain 1) dapat kita tulis sebagai hasil kali suatu himpunan unik bilangan prima, dengan masing-masing bilangan prima ini muncul sebanyak bilangan genap. Misaalnya, (45) ² = 3 . 3 . 3 . 3 . 5 . 5. Pembahasan:
  3. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 43 sepertinya soal-soal selanjutnya banyak berkaitan deh dengan soal sebelumnya,
  4. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 44
  5. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 45
  6. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 46
  7. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 47 Mana di antara yang berikut rasional dan mana yang tak rasional?
  8. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 48 Apakah jumlah dua bilangan takrasional pasti tak rasional? Jelaskan. Sebelum kita ketahui dulu bahwa hasil bagi suatu bilangan takrasional dengan bilangan rasional adalah takrasional Perhatikan pembuktiannya berikut ini Sekarang kita kembali ke soal untuk menjawab apakah jumlah dua bilangan takrasional pasti takrasional
  9. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 49
  10. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 50
  11. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 51
  12. Jawaban atau pembahasan soal Kalkulus dan Geometri Analitis Jilid I, karangan Edwin J. Purcell dan Dale Varberg, soal no. 52  
Label:

Komentar

Posting Komentar

Postingan populer dari blog ini

Pembahasan kalkulus dan geometri analitis edisi kelima jilid 1 bab 1 sub bab 5

Pembahasan Soal Kalkulus Buku Karangan Edwin J. Purcell dan Dale Varberg Bab 1 Sub Bab 5 Jawaban dan pembahasan soal Kalkulus buku karangan Edwin J. Purcell dan Dale Varberg bab 1 sub bab 5 no. 1 (2,-1), (5,3) Penyelesaian: by: sahabat-informasi.com Berdasarkan uraian yang ada pada halaman 26, disebutkan bahwa rumus untuk mencari jarak dua titik adalah didasarkan pada Teorema Pythagoras, garis yang dihubungkan oleh titik (2,-1) dengan titik (5,3) merupakan garis yang tidak sejajar dengan sumbu  x  atau sumbu  y . Untuk dapat menggunakan Teorema Pythagoras kita akan membuat sebuah segitiga siku-siku dengan menjadikan garis yang dihubungkan oleh titik (2,-1) dengan titik (5,3) sebagai sisi miring, sehingga didapat gambar sebagai berikut: Jarak kita simbolkan dengan  d  yang merupakan huruf awal dari kata bahasa Inggris  distance  yang berarti jarak. Jadi dengan menggunakan Teorema Pythagoras jarak antara titik (2,-1) dengan titik (5,3)...
Posting Komentar
Baca selengkapnya

Bilangan Kompleks Anton Rorres

Dalam matematika,  bilangan kompleks adalah bilangan yang berbentuk a + bi di mana a dan b adalah bilangan riil, dan i adalah bilangan imajiner tertentu yang mempunyai sifat i ^2 = −1. Bilangan riil a disebut juga bagian riil dari bilangan kompleks, dan bilangan real b disebut bagian imajiner. Jika pada suatu bilangan kompleks, nilai b adalah 0, maka bilangan kompleks tersebut menjadi sama dengan bilangan real a. Sebagai contoh, 3 + 2i adalah bilangan kompleks dengan bagian riil 3 dan bagian imajiner 2i. Bilangan kompleks dapat ditambah, dikurang, dikali, dan dibagi seperti bilangan riil; namun bilangan kompleks juga mempunyai sifat-sifat tambahan yang menarik. Misalnya, setiap persamaan aljabar polinomial mempunyai solusi bilangan kompleks, tidak seperti bilangan riil yang hanya memiliki sebagian.  
Posting Komentar
Baca selengkapnya